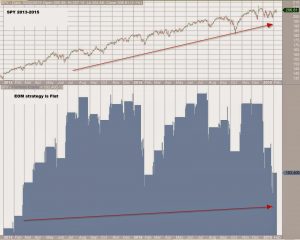
Has the end of month strategy stopped working? Historically and up to 2013, equities have exhibited a positive bias during the end of the month. Here is an example of buying the SPY etf on the first down-day after the 23rd and selling on the first up-day of the next month. Trading is at the same day …
Amibroker
CBA – Quick test drive
Inspiration strategy: http://empiritrage.com/2013/01/21/correlation-based-allocation/ Quoted from Empiritrage.com:“We propose a model that is designed to identify bull-market and bear-market regimes. We examine correlation between stocks and bonds as a signal. Our hypothesis is that negative correlation between long bonds and stocks represents a bear-market regime, and a positive, or non-existent correlation, reflects a bull market regime.The model calculates …
Visualizing Data
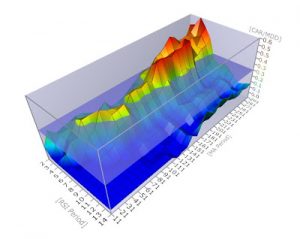
I have been looking for ways to visualize what happens to a trading system when we shift it’s parameters. I bumped into this little free tool that might help us do that. Let’s start from the beginning: We will start with a hypothetical mean reversion system and check visually what happens as the parameters change.We …
Mon AMMI
No, it’s not french and it’s not the movie.It’s a fast-N-rough “Adaptive Multi strategy Multi Instrument” model. Let’s assume we want to trade mean-reversion: If price moves down we buy, if it moves up we sell. Possible Indicators from the blog-o-sphere:RSI(2),RSI(3),RSI(4)DV2 here and hereBSI here or hereBoilingerBandsCRSI hereTD9 here Question 1: Which Indicator to use? One …
Connors RSI – Part 1
One of the readers of this blog, Mark, alerted me to a new indicator/system published from Connors/Alvarez : The ConnorsRSI. What is the ConnorsRSI? It consists of three components:a. Short term Relative Strength, i.e., RSI(3).b. Counting consecutive up and down days (streaks) and “normalizing” the data using RSI(streak,2). The result is a bounded, 0-100 indicator.c. Magnitude of the move …